A última moda da internet é o Pokémon Twitch. Como essas modas evaporam tão rapidamente quanto surgem, vale a pena explicar do que se trata:
O twitch é um site para livestreaming de videogames. Você conecta seu videogame no site, e as pessoas do mundo todo podem te assistir enquanto você joga. Ele tem também uma janela de chat, então as pessoas podem comentar enquanto assistem.
Mas algum gênio aprimorou a idéia original. Ele ligou o twitch em um emulador de Game Boy, e configurou o emulador para pegar o texto do chat e interpretar como se fosse o joystick. Com isso, qualquer um que tenha uma conta lá pode controlar o personagem do jogo (no caso, a versão original de Pokémon). E melhor ainda, como todos estão controlando o mesmo jogo, então o que ele fez foi criar uma espécie de crowdgaming, onde a sabedoria das massas escolhe o melhor caminho do personagem.
Quer dizer, na teoria. Na prática, a internet será a internet. Para cada um que tenta jogar sério, tem um trollzinho que fica mandando o comando oposto. No pico de popularidade, ele chegou a ter mais de cem mil pessoas jogando ao mesmo tempo. Imagine metade disso sacaneando ao invés de jogando, e dá pra ter uma idéia da loucura que é o Pokémon Twitch (ou então leia o FAQ para entender tudo que já aconteceu até agora).
Quando eu fiquei sabendo do Pokémon Twitch, eu fiz o que qualquer pessoa normal faria: criei um modelo matemático do jogo. No meu modelo simplificado, o personagem só anda na vertical, um passo por iteração. O número de jogadores e o número de trolls é o mesmo, então a cada passo ele tem 50% de chance de andar uma unidade para cima ou para baixo. Assuma que ele começa da origem. Nesse modelo, eu faço duas perguntas:
Paradoxalmente, isso está errado! A resposta das duas perguntas é diferente! Probabilidade é um tópico que escapa facilmente da nossa intuição, então vale a pena fazer as contas com cuidado para entender a solução.
Para a resposta da primeira pergunta, vamos calcular qual é o valor esperado da posição. Na iteração 0 ele ainda não executou nenhum movimento, então sabemos a posição deterministicamente: ele está na origem.
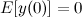
E na iteração n+1? Depende de onde ele estava na iteração n. Tem 50% de chance de ter subido, e 50% de ter descido:
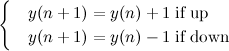
Com isso podemos calcular o valor esperado de y(n+1) direto da lei da expectativa total:
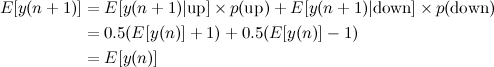
Ou seja, o valor esperado em qualquer iteração é sempre zero, na média nós esperamos que ele fique andando em círculos e nunca fique muito longe da origem.
Entretanto, note que só porque o valor esperado é zero não quer dizer que ele vai sempre terminar na origem: a média é zero, mas a variância não é. Um exercício bastante curioso é calcular qual a probabilidade exata do personagem estar na origem após n iterações. Isso é fácil e dá pra resolver com combinatória de colégio. Imagine que você tem n caixinhas:
Cada uma dessas caixinhas você pode preencher com +1 ou -1; se a soma de todas elas for zero, então o personagem termina na origem. De quantas maneiras podemos fazer isso? Note que nós só precisamos escolher as posições dos +1:
Sabendo onde estão os +1, a posição dos -1 restantes fica unicamente determinada. Precisamos então descobrir de quantas maneiras podemos encaixar n/2 números +1 em n caixinhas. Mas isso é a definição do binomial:
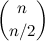
Agora é só dividir pelo total. Como cada caixinha tem duas opções possíveis, +1 e -1, então o número total de caixinhas é 2^n. Portanto, a probabilidade dele terminar na origem é:
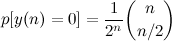
Essa fórmula tem um problema: embora ela seja exata, é muito ruim de calcular quando o n é grande (tente calcular para n=1000, o número de dígitos da sua calculadora vai acabar rapidinho). Podemos achar um assintótico usando a aproximação do coeficiente binomial central:
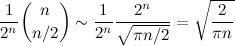
Mais fácil né? Agora podemos calcular facilmente que, para n=1000, a chance de terminar na origem é aproximadamente 2.5%.
Se você tem o olho bom, deve ter percebido uma pegadinha na derivação da fórmula acima. Ela só funciona quando n é par! De fato, quando n é ímpar, não tem como o número de +1 e -1 serem iguais, e portanto a chance dele terminar na origem é zero. Olha que curioso: quando o n é ímpar, ele nunca termina em zero, apesar do valor esperado ser zero!
Vamos agora à segunda pergunta, que é o valor esperado da distância. Por que afinal esse valor é diferente do anterior?
Probabilidade tem uma vantagem grande sobre outros ramos da matemática: é muito fácil conferir as contas. Basta escrever uma simulação computacional com uma quantidade razoável de amostras!
O twitch é um site para livestreaming de videogames. Você conecta seu videogame no site, e as pessoas do mundo todo podem te assistir enquanto você joga. Ele tem também uma janela de chat, então as pessoas podem comentar enquanto assistem.
Mas algum gênio aprimorou a idéia original. Ele ligou o twitch em um emulador de Game Boy, e configurou o emulador para pegar o texto do chat e interpretar como se fosse o joystick. Com isso, qualquer um que tenha uma conta lá pode controlar o personagem do jogo (no caso, a versão original de Pokémon). E melhor ainda, como todos estão controlando o mesmo jogo, então o que ele fez foi criar uma espécie de crowdgaming, onde a sabedoria das massas escolhe o melhor caminho do personagem.
Quer dizer, na teoria. Na prática, a internet será a internet. Para cada um que tenta jogar sério, tem um trollzinho que fica mandando o comando oposto. No pico de popularidade, ele chegou a ter mais de cem mil pessoas jogando ao mesmo tempo. Imagine metade disso sacaneando ao invés de jogando, e dá pra ter uma idéia da loucura que é o Pokémon Twitch (ou então leia o FAQ para entender tudo que já aconteceu até agora).
Quando eu fiquei sabendo do Pokémon Twitch, eu fiz o que qualquer pessoa normal faria: criei um modelo matemático do jogo. No meu modelo simplificado, o personagem só anda na vertical, um passo por iteração. O número de jogadores e o número de trolls é o mesmo, então a cada passo ele tem 50% de chance de andar uma unidade para cima ou para baixo. Assuma que ele começa da origem. Nesse modelo, eu faço duas perguntas:
- Depois de n iterações, onde você espera que o personagem esteja?
- Depois de n iterações, qual você espera que seja a distância do jogador à origem?
Paradoxalmente, isso está errado! A resposta das duas perguntas é diferente! Probabilidade é um tópico que escapa facilmente da nossa intuição, então vale a pena fazer as contas com cuidado para entender a solução.
O valor esperado da posição
Para a resposta da primeira pergunta, vamos calcular qual é o valor esperado da posição. Na iteração 0 ele ainda não executou nenhum movimento, então sabemos a posição deterministicamente: ele está na origem.
E na iteração n+1? Depende de onde ele estava na iteração n. Tem 50% de chance de ter subido, e 50% de ter descido:
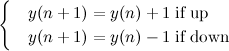
Com isso podemos calcular o valor esperado de y(n+1) direto da lei da expectativa total:
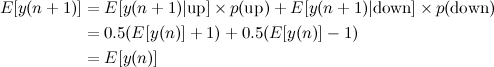
Ou seja, o valor esperado em qualquer iteração é sempre zero, na média nós esperamos que ele fique andando em círculos e nunca fique muito longe da origem.
Entretanto, note que só porque o valor esperado é zero não quer dizer que ele vai sempre terminar na origem: a média é zero, mas a variância não é. Um exercício bastante curioso é calcular qual a probabilidade exata do personagem estar na origem após n iterações. Isso é fácil e dá pra resolver com combinatória de colégio. Imagine que você tem n caixinhas:
Cada uma dessas caixinhas você pode preencher com +1 ou -1; se a soma de todas elas for zero, então o personagem termina na origem. De quantas maneiras podemos fazer isso? Note que nós só precisamos escolher as posições dos +1:
| +1 | +1 | +1 | +1 |
Sabendo onde estão os +1, a posição dos -1 restantes fica unicamente determinada. Precisamos então descobrir de quantas maneiras podemos encaixar n/2 números +1 em n caixinhas. Mas isso é a definição do binomial:
Agora é só dividir pelo total. Como cada caixinha tem duas opções possíveis, +1 e -1, então o número total de caixinhas é 2^n. Portanto, a probabilidade dele terminar na origem é:
Essa fórmula tem um problema: embora ela seja exata, é muito ruim de calcular quando o n é grande (tente calcular para n=1000, o número de dígitos da sua calculadora vai acabar rapidinho). Podemos achar um assintótico usando a aproximação do coeficiente binomial central:
Mais fácil né? Agora podemos calcular facilmente que, para n=1000, a chance de terminar na origem é aproximadamente 2.5%.
Se você tem o olho bom, deve ter percebido uma pegadinha na derivação da fórmula acima. Ela só funciona quando n é par! De fato, quando n é ímpar, não tem como o número de +1 e -1 serem iguais, e portanto a chance dele terminar na origem é zero. Olha que curioso: quando o n é ímpar, ele nunca termina em zero, apesar do valor esperado ser zero!
O valor esperado da distância
Vamos agora à segunda pergunta, que é o valor esperado da distância. Por que afinal esse valor é diferente do anterior?
Para exemplificar, vamos supor que n=2. Em uma das amostras, digamos que os jogadores ganharam e ele andou 2 unidades para cima, então a distância para a origem é 2. Em outra amostra, suponha que os trolls ganharam, então ele andou 2 unidades para baixo. Qual a distância da origem? É 2 também! Distâncias são sempre positivas!
Em outras palavras, o valor esperado da distância é o valor esperado do módulo da posição! E quanto é esse valor? As contas aqui são um pouco mais complicadas, então vou precisar da caixa azul:
Dessa vez nós vamos ter que calcular o valor esperado pela definição:
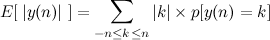
Quando k=0 o somando vale zero também. Vamos então supor k positivo e usar a mesma idéia das caixinhas. A soma era zero quando a quantidade de +1 e de -1 era igual. Dessa vez, nós queremos que a soma seja k, então precisamos ter k números +1 a mais que o número de -1. Portanto, a chance dele terminar em um valor k positivo é:
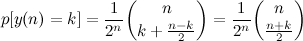
Quando k é negativo, a fórmula é exatamente a mesma! Afinal, é só trocar todos os +1 por -1 e vice versa. Portanto, o valor esperado da distância é:
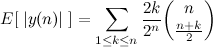
Essa fórmula é difícil de manipular, para deixar mais fácil vamos supor que n é par. Se n é par, podemos escrevê-lo como n=2m. Mas olha só, se n for par, então você nunca vai terminar numa distância k que seja ímpar. Se você tirar k ímpar de n par, o que sobra é ímpar, então não tem como ter soma zero. Portanto podemos supor k par, e fazer k=2q. Substituindo:
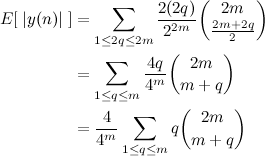
A somatória é uma soma hipergeométrica, então você pode resolvê-la com o algoritmo de Gosper, chegando assim na forma fechada. Mas se você não souber usar o algoritmo de Gosper, não tem problema, é só provar a identidade abaixo por indução finita:
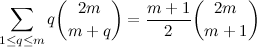
Substituindo a fórmula temos:
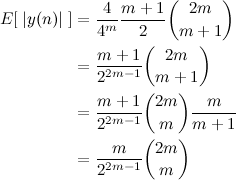
Agora é só usar a aproximação do binomial central:
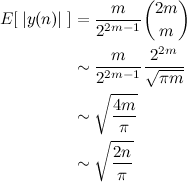
Chegamos então no resultado final, o valor esperado da distância, que é raiz de 2n sobre pi.
Quando k=0 o somando vale zero também. Vamos então supor k positivo e usar a mesma idéia das caixinhas. A soma era zero quando a quantidade de +1 e de -1 era igual. Dessa vez, nós queremos que a soma seja k, então precisamos ter k números +1 a mais que o número de -1. Portanto, a chance dele terminar em um valor k positivo é:
Quando k é negativo, a fórmula é exatamente a mesma! Afinal, é só trocar todos os +1 por -1 e vice versa. Portanto, o valor esperado da distância é:
Essa fórmula é difícil de manipular, para deixar mais fácil vamos supor que n é par. Se n é par, podemos escrevê-lo como n=2m. Mas olha só, se n for par, então você nunca vai terminar numa distância k que seja ímpar. Se você tirar k ímpar de n par, o que sobra é ímpar, então não tem como ter soma zero. Portanto podemos supor k par, e fazer k=2q. Substituindo:
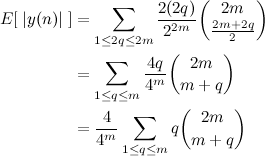
A somatória é uma soma hipergeométrica, então você pode resolvê-la com o algoritmo de Gosper, chegando assim na forma fechada. Mas se você não souber usar o algoritmo de Gosper, não tem problema, é só provar a identidade abaixo por indução finita:
Substituindo a fórmula temos:
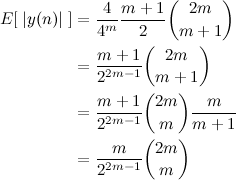
Agora é só usar a aproximação do binomial central:
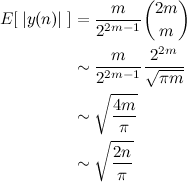
Chegamos então no resultado final, o valor esperado da distância, que é raiz de 2n sobre pi.
A matemática experimental
Probabilidade tem uma vantagem grande sobre outros ramos da matemática: é muito fácil conferir as contas. Basta escrever uma simulação computacional com uma quantidade razoável de amostras!
Eu escrevi um script em python (o código está no github), e os resultados para n=1000 e cem mil amostras foram os seguintes:
- Posição: calculado 0.00, medido 0.05
- Distância: calculado 25.23, medido 25.27
- Término na origem: calculado 2.52%, medido 2.53%
Ou seja, a matemática experimental concordou com a matemática teórica.
A lição que fica dessa brincadeira é tomar muito cuidado com suas intuições sobre probabilidade, porque ela tem uma tendência a nos enganar bem facilmente :)

Nenhum comentário:
Postar um comentário