Eu sei o que você está pensando: "Tá maluco Ricbit? Não dá pra provar um axioma! Eles são proposições tão simples que sua verdade é auto-evidente, não necessitando de prova! Se eu pudesse prová-lo, então não seria um axioma, seria um teorema!"
No fundo, essa é a essência do segundo teorema da incompletude de Gödel: um sistema formal não pode provar sua auto-consistência. Mas tem uma pegadinha aqui. Embora um sistema não possa provar sua auto-consistência, nada impede que você use um sistema mais forte para provar outro sistema mais fraco. Para mostrar como isso pode ser feito, vamos usar como exemplo o mais antigo de todos os axiomas.
O primeiro sistema axiomático foi aquele publicado nos Elementos de Euclides: os cinco postulados que definem as regras da geometria. O axioma que abre a lista não poderia ser mais simples:
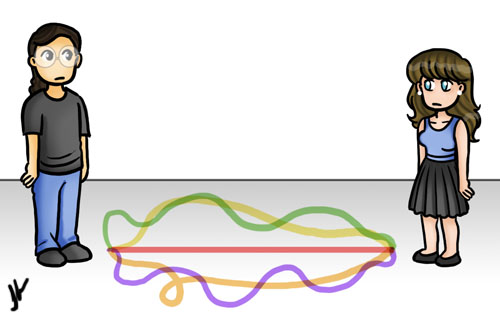
Axioma 1: "Entre dois pontos é sempre possível traçar uma reta".
Mas essa simplicidade é traiçoeira! Na verdade, essa afirmação só faz sentido se você souber de antemão o que é um ponto e o que é uma reta. O Euclides sabia desse problema, por isso, antes de apresentar seus cinco axiomas, ele começa o livro com uma série de 23 definições. Para nós, as definições importantes são as 1, 2 e 4:
Definição 1: "Um ponto é aquilo que não tem parte".
Isso faz sentido. O ponto é o elemento indivisível, o que não pode ser quebrado em pedaços, o átomo. Em linguagem moderna, o ponto é um elemento de dimensão 0.
Definição 2: "Uma linha é um comprimento sem largura".
Isso também faz sentido. A linha é uma coisa comprida e infinitamente fina. Hoje em dia, diríamos que a linha é um elemento de dimensão 1.
Definição 4: "Uma reta é uma linha que se põe igualmente com seus pontos".
E aqui, my friends, é onde a porca torce o rabo. O que raios o Euclides quis dizer com isso? Eu fiquei um tempão tentando interpretar essa frase e não tive sucesso. No desespero, tentei até achar o original em grego, mas mesmo no original a frase é ambígua.
Sem outra alternativa, o jeito foi apelar para alguém que entenda mais que eu. No caso, o grego Proclus, que viveu no século 5 AD, e publicou uma versão comentada dos Elementos. Segundo Proclus, Euclides queria dizer que "de todas as linhas, somente a linha reta ocupa uma distância igual àquela entre seus pontos. Pois a distância de dois pontos entre si é a mesma que o comprimento da linha reta que os tem como extremidades; e esse é o sentido de se pôr igualmente com os seus pontos".
Ou seja, pela interpretação de Proclus, a quarta definição é equivalente a dizer que, de todas as linhas que ligam dois pontos, a reta é a menor delas!
Estritamente falando, essa definição só joga a sujeira debaixo do tapete, porque agora você precisa definir o que é distância. Mas isso já é suficiente para nosso propósito! Nós temos um sistema que define o que é distância: o tensor métrico de Riemann! Se eu assumir que o cálculo sobre os números reais existe, então eu posso usá-los para demonstrar o primeiro axioma de Euclides (ou seja, vou usar um sistema formal mais forte para provar um mais fraco).
Embora o axioma seja simples, as contas para demonstrá-lo não são. Se você fica assustado facilmente com equações diferenciais parciais, pule a caixa azul:
Minha telepatia anda forte ultimamente, então eu ainda sei o que você está pensando: "Pra que isso Ricbit? Você pegou uma proposição da geometria que era intuitiva, e a transformou em um monte de contas horrendas!"
Sim, é verdade. Eu fiz isso de propósito, para ilustrar um ponto importante: pra que você quer se limitar ao que sua intuição alcança? Nós temos à disposição cinco milênios de matemática, eles nos permitem trabalhar com coisas muito além do que nossa intuição consegue visualizar!
Nessas contas da caixa azul nós usamos o tensor métrico para achar o que é uma reta no espaço euclideano. Mas o mesmo raciocínio pode ser usado para achar retas em qualquer tipo de métrica. E sabe quem mais anda em linha reta? A luz!
Mesmo quando o tensor métrico está muito além da minha intuição, como nas proximidades de um buraco negro (onde vale a métrica de Schwarzschild), eu ainda assim sei fazer as contas que me mostram como a luz se comporta por ali. Às vezes até a matemática feia tem sua utilidade :)
No fundo, essa é a essência do segundo teorema da incompletude de Gödel: um sistema formal não pode provar sua auto-consistência. Mas tem uma pegadinha aqui. Embora um sistema não possa provar sua auto-consistência, nada impede que você use um sistema mais forte para provar outro sistema mais fraco. Para mostrar como isso pode ser feito, vamos usar como exemplo o mais antigo de todos os axiomas.
O primeiro axioma de Euclides
O primeiro sistema axiomático foi aquele publicado nos Elementos de Euclides: os cinco postulados que definem as regras da geometria. O axioma que abre a lista não poderia ser mais simples:
Axioma 1: "Entre dois pontos é sempre possível traçar uma reta".
Mas essa simplicidade é traiçoeira! Na verdade, essa afirmação só faz sentido se você souber de antemão o que é um ponto e o que é uma reta. O Euclides sabia desse problema, por isso, antes de apresentar seus cinco axiomas, ele começa o livro com uma série de 23 definições. Para nós, as definições importantes são as 1, 2 e 4:
Definição 1: "Um ponto é aquilo que não tem parte".
Isso faz sentido. O ponto é o elemento indivisível, o que não pode ser quebrado em pedaços, o átomo. Em linguagem moderna, o ponto é um elemento de dimensão 0.
Definição 2: "Uma linha é um comprimento sem largura".
Isso também faz sentido. A linha é uma coisa comprida e infinitamente fina. Hoje em dia, diríamos que a linha é um elemento de dimensão 1.
Definição 4: "Uma reta é uma linha que se põe igualmente com seus pontos".
E aqui, my friends, é onde a porca torce o rabo. O que raios o Euclides quis dizer com isso? Eu fiquei um tempão tentando interpretar essa frase e não tive sucesso. No desespero, tentei até achar o original em grego, mas mesmo no original a frase é ambígua.
Sem outra alternativa, o jeito foi apelar para alguém que entenda mais que eu. No caso, o grego Proclus, que viveu no século 5 AD, e publicou uma versão comentada dos Elementos. Segundo Proclus, Euclides queria dizer que "de todas as linhas, somente a linha reta ocupa uma distância igual àquela entre seus pontos. Pois a distância de dois pontos entre si é a mesma que o comprimento da linha reta que os tem como extremidades; e esse é o sentido de se pôr igualmente com os seus pontos".
Ou seja, pela interpretação de Proclus, a quarta definição é equivalente a dizer que, de todas as linhas que ligam dois pontos, a reta é a menor delas!
Estritamente falando, essa definição só joga a sujeira debaixo do tapete, porque agora você precisa definir o que é distância. Mas isso já é suficiente para nosso propósito! Nós temos um sistema que define o que é distância: o tensor métrico de Riemann! Se eu assumir que o cálculo sobre os números reais existe, então eu posso usá-los para demonstrar o primeiro axioma de Euclides (ou seja, vou usar um sistema formal mais forte para provar um mais fraco).
Embora o axioma seja simples, as contas para demonstrá-lo não são. Se você fica assustado facilmente com equações diferenciais parciais, pule a caixa azul:
Vamos começar com o tensor métrico de Riemann. Na geometria euclideana, ele é o próprio teorema de Pitágoras:
Nós podemos multiplicar e dividir por dx^2 (sim, eu sei), e depois tirar a raiz quadrada dos dois lados:
Vamos supor que a função final será y=f(x). Então dy/dx é a derivada de f(x). E nesse ponto podemos integrar dos dois lados:
Se a linha entre A e B é descrita pela função f(x), então seu comprimento será S. O nosso objetivo é achar a função f(x) que minimiza S.
Quem já estudou cálculo deve estar pensando "é só derivar e igualar a zero!". A intuição é essa mesmo, mas os detalhes são diferentes. Nós não queremos achar um ponto que minimiza uma função, queremos achar uma função que minimiza uma integral.
Esse tipo de problema é resolvido pelo Cálculo de Variações. A teoria em geral é bastante complicada, mas nesse caso em específico tem uma fórmula que resolve o problema sozinha, a equação de Euler-Lagrange. A sua forma é a seguinte: suponha que você tenha uma função L[x, f(x), f'(x)]. Então o extremo da integral abaixo...
.. é dado pela solução dessa equação diferencial:
No nosso caso, a função L[x, f(x), f'(x)] é dada por:
Agora eu vou fazer as contas em câmera lenta porque elas são levemente diferentes do cálculo normal que estamos acostumados. O primeiro termo da equação é zero, porque L é constante em relação a f(x). Confira: na expressão de L, aparece f'(x), mas não aparece f(x).
Para a segunda derivada parcial, é só aplicar a regra da cadeia. Esse passo tem uma pegadinha:
Peraí, ali na segunda linha não tinha que multiplicar pela derivada segunda de f? Teria, se você estivesse derivando em relação a x, mas você está derivando em relação a f'(x)! Podemos fazer a última derivada agora:
Agora é só plugar na equação original:
Opa, o denominador é sempre positivo, então dá pra jogar fora!
Tcharam! A menor linha que liga dois pontos realmente é uma reta! Mas ainda não acabou, falta provar que a reta é única. Isso vem direto das condições de contorno:
Pronto, C1 e C2 são unicamente definidos pelos pontos nas extremidades, então a reta que os une é única. QED.
Nós podemos multiplicar e dividir por dx^2 (sim, eu sei), e depois tirar a raiz quadrada dos dois lados:
Vamos supor que a função final será y=f(x). Então dy/dx é a derivada de f(x). E nesse ponto podemos integrar dos dois lados:
Se a linha entre A e B é descrita pela função f(x), então seu comprimento será S. O nosso objetivo é achar a função f(x) que minimiza S.
Quem já estudou cálculo deve estar pensando "é só derivar e igualar a zero!". A intuição é essa mesmo, mas os detalhes são diferentes. Nós não queremos achar um ponto que minimiza uma função, queremos achar uma função que minimiza uma integral.
Esse tipo de problema é resolvido pelo Cálculo de Variações. A teoria em geral é bastante complicada, mas nesse caso em específico tem uma fórmula que resolve o problema sozinha, a equação de Euler-Lagrange. A sua forma é a seguinte: suponha que você tenha uma função L[x, f(x), f'(x)]. Então o extremo da integral abaixo...
.. é dado pela solução dessa equação diferencial:
No nosso caso, a função L[x, f(x), f'(x)] é dada por:
Agora eu vou fazer as contas em câmera lenta porque elas são levemente diferentes do cálculo normal que estamos acostumados. O primeiro termo da equação é zero, porque L é constante em relação a f(x). Confira: na expressão de L, aparece f'(x), mas não aparece f(x).
Para a segunda derivada parcial, é só aplicar a regra da cadeia. Esse passo tem uma pegadinha:
Peraí, ali na segunda linha não tinha que multiplicar pela derivada segunda de f? Teria, se você estivesse derivando em relação a x, mas você está derivando em relação a f'(x)! Podemos fazer a última derivada agora:
Agora é só plugar na equação original:
Opa, o denominador é sempre positivo, então dá pra jogar fora!
Tcharam! A menor linha que liga dois pontos realmente é uma reta! Mas ainda não acabou, falta provar que a reta é única. Isso vem direto das condições de contorno:
Pronto, C1 e C2 são unicamente definidos pelos pontos nas extremidades, então a reta que os une é única. QED.
Minha telepatia anda forte ultimamente, então eu ainda sei o que você está pensando: "Pra que isso Ricbit? Você pegou uma proposição da geometria que era intuitiva, e a transformou em um monte de contas horrendas!"
Sim, é verdade. Eu fiz isso de propósito, para ilustrar um ponto importante: pra que você quer se limitar ao que sua intuição alcança? Nós temos à disposição cinco milênios de matemática, eles nos permitem trabalhar com coisas muito além do que nossa intuição consegue visualizar!
Nessas contas da caixa azul nós usamos o tensor métrico para achar o que é uma reta no espaço euclideano. Mas o mesmo raciocínio pode ser usado para achar retas em qualquer tipo de métrica. E sabe quem mais anda em linha reta? A luz!
Mesmo quando o tensor métrico está muito além da minha intuição, como nas proximidades de um buraco negro (onde vale a métrica de Schwarzschild), eu ainda assim sei fazer as contas que me mostram como a luz se comporta por ali. Às vezes até a matemática feia tem sua utilidade :)

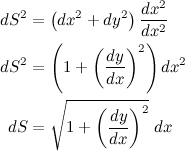
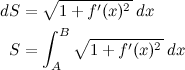
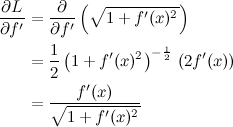
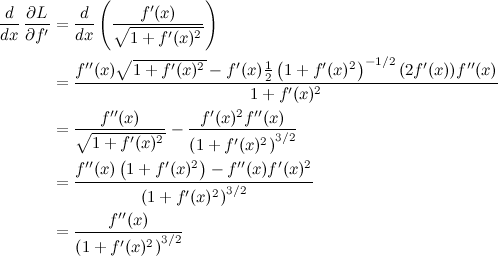
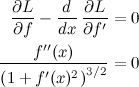
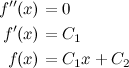
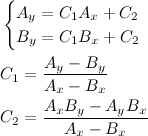
Nenhum comentário:
Postar um comentário