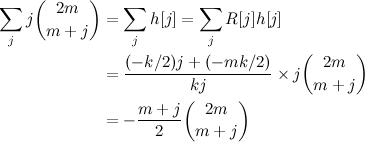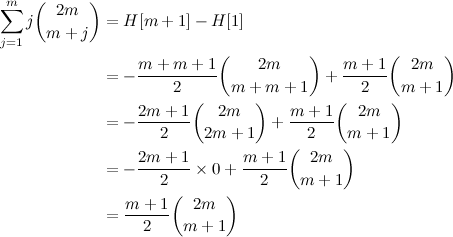Matemática x Tanques de Guerra

Quando eu era criança pequena lá na década de 80, eu tinha um brinquedo de tanque de guerra. Ele chamava Panzer, e era fabricado pela brinquedos Mimo. Para a época era bem divertido: tinha controle remoto, e, além de andar, ainda disparava mísseis!

Mas eu não percebia a ironia do brinquedo. O Panzer não era só um brinquedo, ele existiu de verdade. Na vida real, o Panzer era uma máquina nazista de destruição. A série Panzer de tanques alemães foi responsável pela morte direta de incontáveis aliados. Ver um Panzer surgindo no horizonte era como ver a morte vindo em sua direção. Era um mimo esse Panzer.

Por outro lado, o Panzer era forte, mas não era invencível. Os aliados tinham armas capazes de deter o Panzer, o problema era descobrir quantas dessas armas eles deveriam levar para o front. Poucas semanas antes do Dia D, os alemães começaram a usar o novo modelo Panzer V, e os aliados não tinham como estimar quantas armas levar sem saber quantos Panzer V os inimigos fabricaram.

Foi então que os aliados usaram a arma definitiva contra o Panzer: a Matemática! Usando um truque muito esperto, eles estimaram que os alemães estavam fabricando 270 Panzers por mês. Depois que a guerra acabou, eles foram nos arquivos alemães conferir os números, e na verdade estavam fazendo 276 Panzers por mês. A estimativa foi muito boa!

A Quantidade de Tanques

O truque dos aliados se baseava em um erro dos alemães e em uma hipótese estatística. O erro dos alemães era que os tanques tinham número de série sequencial. Quando saíam da fabrica, eram numerados como 1, 2, 3, e assim por diante. Ao fazer isso, eles deixaram uma brecha para os hackers aliados.

Suponha que você capturou um Panzer alemão, e o serial dele era 14. Você consegue estimar quantos tanques eles produziram baseado só nesse número? No caso geral não, mas você pode fazer uma hipótese simplificadora, que é supor que o tanque que você capturou é aleatório (ou seja, os alemães estavam distribuindo igualmente os tanques por toda a Europa).

Com essa hipótese a intuição é clara. Vamos supor, hipoteticamente, que os alemães fizeram 200 tanques. Qual chance de você capturar um tanque de serial menor ou igual a 14 nessa situação? É 14/200 né? E se os alemães fizeram só 20 tanques? Aí a chance é 14/20, dez vezes maior que 14/200. Com a hipótese de tanque aleatório, é mais provável que os alemães tenham feito 20 tanques do que 200 tanques.

Você pode formalizar esse argumento usando o teorema de Bayes, e calcular o valor esperado do número de tanques. Vamos fazer as contas na caixa azul:

Suponha que conseguimos capturar k tanques. Dentre esses k tanques, o maior serial encontrado tem o valor m. Com essas informações, vamos calcular qual é o valor esperado do número de tanques produzidos, que vamos chamar de n. Podemos abrir esse valor esperado pela definição:
$$E[n\;|\;m,k] = \sum_{n} n \; p(n\; |\; m,k)$$
O problema então é achar a probabilidade condicional de n, dados m e k. Nós ainda não sabemos quanto vale essa probabilidade, mas podemos abri-la usando o teorema de Bayes:
$$p(n\;|\;m,k)=\frac{p(m,k\;|\;n)\;p(n)}{p(m,k)}$$
Essas três probabilidades nós conseguimos calcular! A primeira delas, p(m,k|n), sai por combinatória. Dado um vetor de tamanho n, de quantas maneiras conseguimos escolher k elementos, de modo que o maior deles seja m?

Um dos elementos precisa necessariamente ser o m, então só precisamos calcular a posição dos outros k-1 restantes. E eles precisam ser menores que m, então só podem estar nas m-1 posições menores que m. Por isso, essa quantidade vale binomial(m-1, k-1). Note, entretanto, que isso só vale quando n>=m, caso contrário a probabilidade é zero (não tem como o máximo ser m se o vetor tem um tamanho menor que m).

Para calcular a probabilidade desejada, temos que achar de quantas maneiras podemos escolher k elementos dentre n, sem considerar a restrição do maior deles ser m. Mas isso é o próprio binomial(n, k). Então, a probabilidade é:
$$p(m,k\;|\;n) = \frac{\displaystyle{m-1\choose k-1}} {\displaystyle{n\choose k}}[n\ge m]$$
Vamos agora para a segunda, p(n). Eu não tenho nenhuma informação sobre quantos tanques foram produzidos, então não sei qual é a probabilidade de ter n tanques. Mas eu posso chutar que a distribuição é uniforme. A chance de ter 15 tanques, ou de ter 500 tanques, a priori, deve ser a mesma. Por isso, vamos fazer p(n) ser uma constante independente de n:
$$p(n)=c$$
A última, p(m,k), é a probabilidade do máximo ser m em k escolhas, independente do valor de n. Para isso, podemos usar a lei da probabilidade total: 
$$p(m,k) = \sum_n p(m,k\;|\;n) \;p(n)$$ 
Essas duas já sabemos calcular! É só substituir:
 $$\begin{align*} p(m,k) &= \sum_n p(m,k\;|\;n) \;p(n) \\ &= \sum_n \frac{{m-1\choose k-1}} {{n\choose k}}[n\ge m]\;c\\ &= \sum_{n\ge m} c {m-1\choose k-1} {n\choose k}^{-1}\\ &= c {m-1 \choose k-1} \sum_{n\ge m} {n\choose k}^{-1}\\ \end{align*} $$
A somatória tem uma forma fechada, que você pode achar com o algoritmo de Gosper:
$$\sum_{n=m}^{\infty}{n\choose k}^{-1}=\frac{m}{k-1}{m\choose k}^{-1}$$ 
Substituindo:
$$\begin{align*} p(m,k) &= c {m-1 \choose k-1} \sum_{n\ge m} {n\choose k}^{-1}\\ &= c {m-1 \choose k-1} \times \frac{m}{k-1}{m\choose k}^{-1} \\ &= \frac{cm}{k-1} {m-1 \choose k-1} {m\choose k}^{-1} \\ \end{align*} $$
Agora podemos voltar e substituir as três probalidades na fórmula de Bayes:
$$ \begin{align*} p(n\;|\;m,k)&=\frac{p(m,k\;|\;n)\;p(n)}{p(m,k)} \\ &= \frac{\displaystyle{m-1\choose k-1}{n\choose k}^{-1}[n\ge m]\times c} {\displaystyle\frac{cm}{k-1}{m-1\choose k-1}{m\choose k}^{-1}}\\ &= \frac{k-1}{m}{m\choose k}{n\choose k}^{-1}[n\ge m] \end{align*}$$
Por fim, podemos substituir na fórmula do valor esperado:
 $$\begin{align*} E[n\;|\;m,k] &= \sum_{n} n \; p(n\; |\; m,k)\\ &= \sum_n n \frac{k-1}{m}{m\choose k}{n\choose k}^{-1}[n\ge m]\\ &= \frac{k-1}{m}{m\choose k}\sum_{n\ge m} n {n\choose k}^{-1}\\ \end{align*}$$
Essa somatória também tem uma forma fechada por Gosper:
$$ \sum_{n=m}^{\infty} n{n\choose k}^{-1}=\frac{m(m-1)}{k-2}{m\choose k}^{-1}$$
Chegamos então na substituição final:
$$\begin{align*} E[n\;|\;m,k] &= \frac{k-1}{m}{m\choose k}\sum_{n\ge m} n {n\choose k}^{-1}\\ &= \frac{k-1}{m}{m\choose k}\times\frac{m(m-1)}{k-2}{m\choose k}^{-1} \\ &= \frac{(k-1)(m-1)}{k-2} \\ \end{align*}$$

A Estimativa na Prática

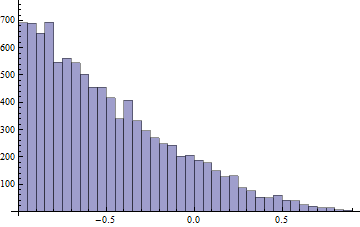
A fórmula final é super simples, mas ela funciona mesmo na prática? Podemos testá-la fazendo uma simulação numérica. Para isso, eu fiz dez mil simulações. Em cada uma eu sorteio o número de tanques fabricados, e escolho aleatoriamente 3 deles. Aí eu calculo a estimativa pela fórmula, e normalizo o erro. O código está no github, e o histograma resultante é o abaixo. A normalização é tal que o valor 0 é uma estimativa totalmente correta:

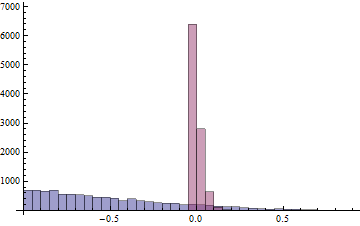
A estimativa não ficou muito boa não! Ao invés de ter uma gaussiana em torno do zero, o estimador tem um bias muito forte para os negativos. Felizmente, esse problema só acontece porque capturamos apenas 3 tanques. Se, ao invés disso, tivéssemos capturado 30 tanques, então o histograma seria bem melhor. Compare o histograma de 30 tanques sobreposto ao de 3 tanques:

Bem melhor né? Agora quase todas as estimativas estão bem próximas do zero. Esse método é bastante sensível ao número de tanques capturados. Os aliados sabiam disso, por isso que a estimativa deles foi tão boa (estimaram 270 tanques/mês, quando o valor real era 276). Sabe quantos tanques eles capturaram para fazer essa estimativa? Só dois tanques!

Claro que tem um truque. A estimativa com dois tanques é muito ruim, mas eles notaram que os alemães colocavam serial em todas as peças do tanque. Em especial, cada tanque tinha 48 rodas, cada uma com um serial único. Por isso, eles conseguiram usar a fórmula com k=96, o que deu a precisão alta que queriam. E no fim a matemática ganhou a guerra :)

O Objetivo Final da Matemática

Quem acompanhou as contas na caixa azul do post sobre o Pokèmon Twitch deve ter notado que eu pulei um pedaço. Em certo ponto da demonstração, eu magicamente tirei do chapéu uma fórmula nada óbvia:

E como foi que eu cheguei nessa fórmula? Simples, eu calculei no Wolfram Alpha:

"Ricbit, você trapaceou! Que roubalheira! Um matemático de verdade jamais faria isso!"

Mas será que é trapaça mesmo? Nesse post, eu vou mostrar como se resolve essa conta sem usar o Wolfram Alpha; e, se você acha que é trapaça, talvez acabe mudando de idéia :)

A progressão hipergeométrica

Para resolver essa somatória sem usar o Wolfram Alpha, nós precisamos relembrar as progressões que aprendemos no colégio. A primeira delas foi a progressão aritmética, onde a diferença entre dois números consecutivos é constante:

   

A segunda delas é a progressão geométrica, onde a razão entre dois números consecutivos é constante:

   

Uma progressão extremamente útil que não ensinam no colégio é a progressão hipergeométrica. Ela parece com a progressão geométrica, porque é definida a partir da razão entre dois elementos consecutivos. Mas agora, ao invés dessa razão ser constante, nós permitimos que a razão seja uma função racional (que é só um jeito chique de dizer que ela é o quociente entre dois polinômios):

 

Naquela somatória que queremos resolver, os termos sendo somados formam uma progressão hipergeométrica. Confira:

   

O numerador é um polinômio em q, o denominador é um polinômio em q. Então confere com a nossa definição de progressão hipergeométrica.

A soma da progressão hipergeométrica

Certamente vocês lembram que as progressões do colégio tinham uma fórmula para a soma de seus termos. A soma dos n primeiros termos da progressão aritmética é:

A soma dos n primeiros termos da progressão geométrica é:

 

A soma dos n primeiros termos da progressão hipergeométrica é... oops! Não existe uma fórmula geral para a soma de termos hipergeométricos.

Antigamente, achar uma fórmula para uma soma hipergeométrica era tão raro que elas até ganhavam nomes especiais. Por exemplo, a igualdade abaixo tem um nome, é o Binômio de Newton:

 

Outras somas hipergeométricas não tem fórmula, mas são tão úteis, que a própria soma ganha um nome e passa a valer como se fosse uma fórmula:

Por muitos séculos esse foi o estado da arte. Alguém acha uma fórmula aqui, alguém nomeia uma soma ali. Mas isso mudou no meio do século 20.

O algoritmo de Gosper

O primeiro progresso na direção de um método geral de resolução de somas hipergeométricas foi feito pela Mary Celine Fasenmyer em 1945. Depois de se formar em matemática, ela se juntou à ordem religiosa Sisters of Mercy (sim, a mesma que inspirou o nome da banda), e lá ela criou o Método da Irmã Celine, um algoritmo que consegue resolver automaticamente alguns tipos de somas hipergeométicas.

Em 1978 o método foi aprimorado por Bill Gosper e se tornou o algoritmo de Gosper (muito embora eu desconfie que, se a Irmã Celine fosse homem, o algoritmo seria de Gosper-Celine). O método de Gosper se baseia em um teorema surpreendente: A solução de uma soma hipergeométrica é outro hipergeométrico, se e somente se ela puder ser escrita na forma abaixo, onde R[j] é uma função racional.

Essa somatória parece esquisita. Se j é o índice da somatória, então o que ele está fazendo no lado direito da equação? E cadê os limites da somatória?

A resposta é que essa é uma somatória indefinida. Funciona do mesmo jeito que no cálculo: lá você tem integrais definidas e integrais indefinidas, aqui nós temos somatórias definidas (com limites), e somatórias indefinidas (sem limites). Para uma somatória indefinida, sempre vale a propriedade abaixo:

 

Essas duas equações são tudo que nós precisamos para usar o algoritmo de Gosper. Vamos à caixa azul calcular a nossa somatória original:

Começamos substituindo uma equação na outra:

Podemos então dividir tudo por h[j]:

 

Opa, a razão entre os h nós já calculamos lá em cima para a nossa somatória!

 

Falta achar R[j]. Eu sei que ele é um quociente de polinômios, mas não sei qual o grau desses polinômios. Eu vou chutar que o grau é 1, se der errado depois eu volto e aumento o grau. Pois bem, se o grau é 1, então R[j] é da forma abaixo:

 

Agora eu vou substituir. Aperte o cinto que lá vem turbulência:

   

O resultado é um polinômio gigante em j que é identicamente nulo. Se ele é identicamente nulo, então cada um dos seus coeficientes precisa ser zero. Com isso podemos montar um sistema de equações:

 

Agora é "só" resolver o sistema! Vou poupá-los de páginas e páginas, o resultado é o seguinte:

   

Se o sistema não tivesse solução, eu teria que voltar lá em cima e aumentar o grau do polinômio (se as contas foram titânicas com grau 1, imagine com grau 2). Mas o processo não é infinito, existem métodos que permitem achar um limite superior para o grau do polinômio. Se você atingir esse limite sem achar nenhuma solução, então você provou que sua somatória não pode ser escrita como um hipergeométrico.

Voltando à nossa equação original, agora nós sabemos quanto vale a somatória indefinida:

   

Nós queremos a soma de 1 até m, então precisamos converter a soma indefinida em uma soma definida, usando o teorema fundamental do cálculo discreto:

 

Aplicando o teorema, temos:

   

Pronto, esse é o resultado final. Eu acho muito importante que a pessoa resolva o algoritmo de Gosper uma vez na vida, para nunca mais cometer a sandice de repetir o processo. O método é mecânico, você só precisa seguir as regras e não errar as contas. O computador faz isso melhor que você. Use o Wolfram Alpha e economize grafite.

O objetivo final da Matemática

No final do século 19, o Bertrand Russell e o Alfred Whitehead tiveram uma idéia. Ele bolaram um plano para axiomatizar toda a matemática, de uma maneira completa e livre de contradições. Se o plano funcionasse, então toda a Matemática seria reduzida à manipulação de símbolos, que é um processo puramente mecânico e automatizável. O plano começou muito bem, a ponto do Whitehead fazer a seguinte declaração:

"A Civilização avança estendendo o número de operações importantes que podemos fazer sem ter que pensar."

Baseado nessa citação, o Concrete Mathematics do Knuth vai além e conclui:

"O objetivo final da matemática é eliminar a necessidade de todo pensamento inteligente."

É verdade, o objetivo sempre foi esse. Para os babilônios, resolver uma equação de segundo grau era dificílimo, só os grandes mestres conseguiam. Hoje em dia, nós transformamos a equação de segundo grau em uma fórmula que é ensinada para crianças de 14 anos. Você não precisa ser inteligente para usar a fórmula, é só substituir os números e fazer as contas.

Imagine se fosse possível fazer isso com toda a matemática, ao invés de só com equações de segundo grau! Você poderia usar computadores para fazer as contas, no lugar de crianças de 14 anos. A Matemática seria um problema resolvido, e aí você pode se concentrar no que interessa, que são as aplicações. Um físico acabou de descobrir uma propriedade quântica nova, será que ela permite criar um aparelho de teletransporte? Eu monto a equação, jogo no computador, e tcharam! Está aqui a resposta!

Toda a saga por trás do plano do Russell e do Whitehead é contada em quadrinhos no fabuloso Logicomix. Infelizmente, o final da história é que o plano falhou. E falhou espetacularmente. Em 1931, o Gödel provou que nenhum sistema axiomático é capaz de provar todas as sentenças verdadeiras que é capaz de descrever, acabando de uma vez por todas com o sonhado plano da axiomatização completa.

E o século 20 desceu ladeira abaixo. O Church provou que, mesmo se a axiomatização completa tivesse tido sucesso, seria impossível criar um método que prove um teorema qualquer a partir dos axiomas. O Turing provou que é impossível criar um método que analise um programa de computador e diga se ele termina ou se entra em loop infinito. O Matiyasevich provou que é impossível criar um método que resolva todas as equações diofantinas. O Richardson provou que é impossível criar um método que prove todas as identidades trigonométricas. Foi o fim da matemática automatizada... ou não?

Claro que não! Todos esses teoremas provam a impossibilidade do caso geral. Mas você sempre pode automatizar um caso específico. Não existe uma fórmula geral para a soma hipergeométrica, mas o algoritmo de Gosper prova que pelo menos um caso especial pode ser automatizado: o caso da soma hipergeométrica cujo resultado também é um termo hipergeométrico. E esse caso é imensamente útil na prática, especialmente se você estuda computação ou combinatória.

E no fim das contas, usar o Wolfram Alpha para resolver uma somatória é trapacear ou não? Por dentro, tudo que o Wolfram Alpha faz é usar o algoritmo de Gosper. Se você acredita que usar um método computacional é roubar, então por consistência precisa abrir de mão de todos os outros métodos computacionais. Não pode mais resolver a equação de segundo grau usando a fórmula de Bhaskara, não pode mais calcular o máximo divisor comum com o algoritmo de Euclides, não pode nem calcular quanto é 463 vezes 367 sem antes decorar a tabuada do 367.

Para mim isso não faz sentido. E por isso eu uso o Wolfram Alpha sem medo de ser feliz :)