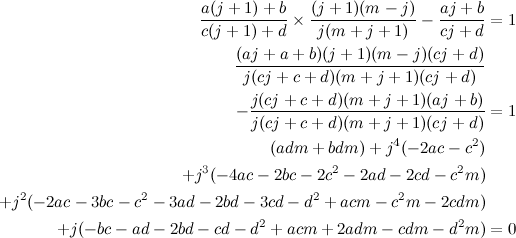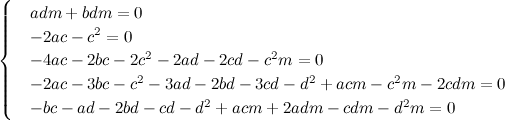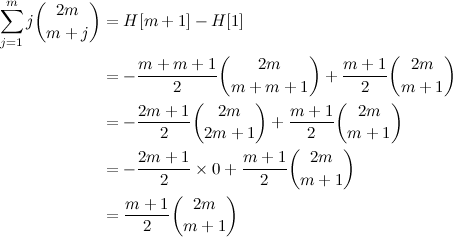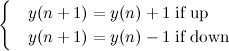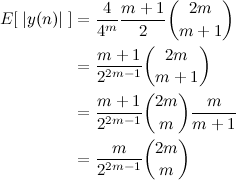No mês de maio eu completei cinco anos de casado! Quando eu casei, aproveitei a lua-de-mel em Paris para falar sobre a ciência da Torre Eiffel, então nada mais apropriado que aproveitar o aniversário para falar sobre outro mistério da torre: a equação que descreve o seu formato!
O desafio proposto pelo Gustave Eiffel era grandioso: construir a torre mais alta do mundo. Na época, o recorde era o Monumento de Washington, com 169 metros. O Eiffel pretendia erguer sua torre com 324 metros, quase o dobro do recorde anterior.
Para entender o desafio, vale a pena comparar a Torre Eiffel com outras torres da antiguidade. O desenho abaixo está em escala, e mostra a Torre Eiffel comparada com a Grande Pirâmide de Giza no Egito, e com o Campanário de São Marcos em Veneza:
O primeiro desafio ao fazer uma torre é garantir que ela consiga suportar seu próprio peso. Os egípcios resolveram isso com força bruta: usaram blocos de pedra maciços e fizeram a base bem maior que o topo. O resultado final certamente funcionou, a pirâmide está aí de pé 4500 anos depois. Mas ela é um desperdício de material, com tecnologia moderna você não precisa de tanta matéria-prima para chegar nessa altura.
O Campanário de São Marcos é o extremo oposto. Ele foi construído em 1514, e nessa época a tecnologia já permitia criar uma torre com a largura da base igual à do topo. O problema é que a torre caiu! Em 1902 ela não resistiu ao próprio peso e colapsou (nenhuma vida humana foi perdida, mas o gato do zelador morreu). A torre que você visita hoje em Veneza é uma reconstrução.
Como fazer, então, uma torre alta que suporte o próprio peso? O Eiffel sabia a resposta porque tinha experiência no assunto. Antes de criar os ícones pelo qual é mais lembrado, ele construía pontes. Existem pontes do Eiffel por todo o mundo, desde a França e a Romênia, até o Vietnã e o Chile.
Para entender a tecnologia do Eiffel, vale a pena comparar com uma ponte antiga: a Pont du Gard, um aqueduto romano construído dois mil anos atrás. Ele cobre uma distância de 275 metros a uma altura de 48 metros. Para isso, ela precisa de cinco apoios no chão e três níveis de arcos para aguentar seu próprio peso:
Agora, compare com uma das mais belas pontes construídas pelo Eiffel: a Ponte Dona Maria, na Cidade do Porto, em Portugal. Ela cobre 353m a 60m de altura, em ambos os casos maior que a ponte romana. E faz isso usando só dois apoios no chão! O segredo do Eiffel para conseguir esse feito é a magia da treliça. Ao usar uma treliça, você consegue suportar mais peso com menos material.
Todo mundo sabia que o Eiffel era expert no assunto, e que ele saberia construir uma torre que suportasse o próprio peso. Mas, ainda assim, na época ele ouviu muitas críticas. Uma coisa é você construir uma ponte na horizontal, outra é construir uma torre na vertical. Estruturas na vertical tem um problema adicional: será que o Eiffel sabia como fazer a torre resistir ao vento?
Quando a torre ficou pronta, o Eiffel calou os críticos. Quem já visitou a torre sabe que no terceiro piso venta. Venta muito mesmo! Porém, a torre não se abala. Fica lá, imóvel, mesmo com os ventos mais fortes.
E qual foi o truque do Eiffel para deixar a torre tão estável com o vento? Até pouco tempo atrás, ninguém sabia. As plantas da torre Eiffel são conhecidas, você pode ver todas as especificações em um livrão publicado pela Taschen (todas mesmo, tem até o diâmetro e comprimento de cada parafuso). Mas as plantas não falam o truque da estabilidade, tudo que dizem é que o Eiffel determinou o formato da torre de forma a minimizar a ação do vento, e fez isso usando "métodos geométricos baseados em observações empíricas".
O formato da torre foi um mistério por mais de um século, até que Patrick Weidman, professor da Universidade de Colorado, matou o problema, e da maneira mais simples possível. Ele foi atrás dos diários do Eiffel e achou lá a dica que resolve o problema! O trecho do diário dizia:
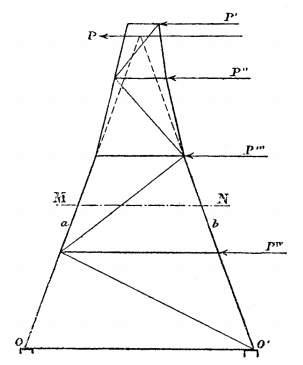
"Suponha que as faces de uma treliça simples formam uma parede resistente às forças cisalhantes do vento, cujas componentes horizontais são P', P'', P''', P''''. Sabemos que, para calcular as forças atuantes no corte pelo plano MN, precisamos determinar a resultante P de todas as forças exteriores atuando acima da secção, e decompor essa resultante nas três forças passando pelas peças cortadas. Se a forma do sistema for tal que, para cada corte horizontal MN, a extensão das peças externas da treliça se intersectam na força exterior P, então as forças na barra interna serão zero e podemos excluir esse membro."
O diário tinha esse desenho acompanhando:
Lendo com cuidado dá para entender direitinho a motivação do formato da torre. Vamos recriar o raciocínio em câmera lenta. Nós começamos supondo que o vento é uma carga horizontal atuando sobre toda a torre (que ele representou como as forças P', P'', etc). O truque agora é pegar um corte horizontal arbitrário (que ele chamou de MN), e tirar toda a parte de cima da torre. As forças na estrutura não mudam se substituirmos a parte de cima por um ponto material de mesma massa, localizado no centróide do que foi tirado.
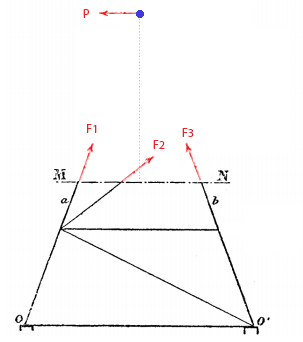
Vamos então ver qual é o efeito do vento. Eu tenho uma força P horizontal, que é a resultante do vento. Tenho ainda três forças F1, F2, F3, que são as forças atuando sobre as vigas da treliça. Quando uma treliça está em equilíbrio, as forças sobre ela são sempre de tração ou compressão, ou seja, estão na mesma direção de suas vigas respectivas.
A torre está em equilíbrio estático, logo a soma das forças é zero. Além disso, ela também não está rotacionando; logo a soma dos torques também é zero. O torque é o produto da força pela distância; mas não é qualquer distância, é a distância na direção perpendicular à força.
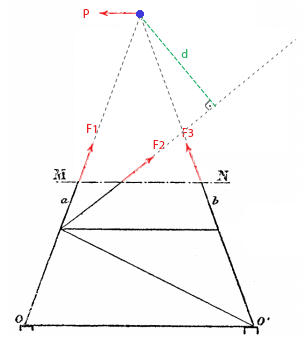
Agora o truque do Eiffel é claro. Ele construiu as laterais da torre de modo que as tangentes às vigas mais externas sempre passam pelo centróide. Quando você faz isso, a direção das forças P, F1 e F3 apontam para o centróide, então o torque delas é zero. Só a força F2 está aplicando torque no centróide!
Podemos calcular a soma dos torques agora. A distância associada à força F2 é a distância d, em verde na figura. Note que ela é estritamente positiva.
$$\begin{align*} P\times 0 +F_1\times 0+F_2\times d+F_3\times 0&=0\\ F_2\times d&=0\\ F_2&=0 \end{align*}$$
Ahá! Se as tangentes externas apontam para o centróide, então a força na viga interna é zero! Se o vento horizontal fosse a única força atuando sobre a torre, então nós poderíamos até tirar a viga interna que não faria diferença!
É claro que na prática não podemos tirar a viga. Ela não ajuda a resistir ao vento, mas ajuda a sustentar o peso. Por outro lado, essa viga pode ser mais fraca que as outras. Com a idéia do Eiffel, só as vigas externas precisam ser fortes. Nessa foto que eu tirei do pilar oeste isso é bem visível: as vigas externas são largas e feitas de material rígido, enquanto que as internas são finas e feitas de mini-treliças, o que deixa a estrutura como um todo mais leve. E quanto mais leve, mais alto você pode subir.
Agora que nós sabemos o truque do Eiffel, podemos calcular qual é o lugar geométrico dos pontos cujas tangentes passam pelo centróide, isso vai nos dar a equação que descreve o fomato da torre. Aparentemente o Eiffel nunca precisou fazer isso, já que ele usou "um método geométrico baseado em observações empíricas" (para mim isso é um jeito de dizer que ele calculou uma solução numérica ao invés de resolver a equação de fato).
Mas ele poderia ter resolvido a equação se quisesse. Vamos fazer as contas na caixa azul para conferir, pule se você tem medo de equações diferenciais:
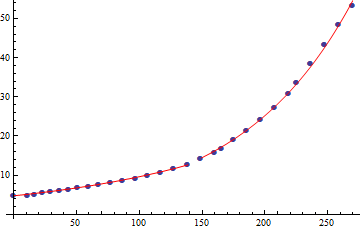
Agora que sabemos qual o formato teórico da torre, podemos usar os dados reais da torre para estimar os coeficientes da exponencial. Eu rodei um best fit e cheguei em A=3.34323 e B=0.0102592:
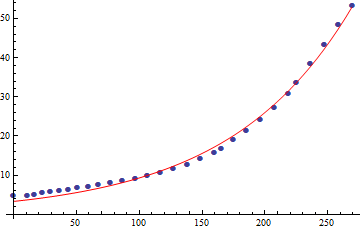
A aproximação é boa, mas... parece que não encaixa direitinho? É meio frustrante fazer esse monte de contas, e no fim a curva real não ser tão parecida assim com a equação deduzida.
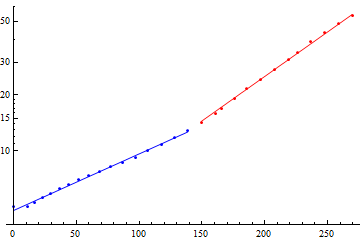
Mas tem um motivo para isso, e o motivo é que o Eiffel era engenheiro, não matemático. Quando você plota uma exponencial em um gráfico semi-log, o resultado tem que ser uma linha. Mas olha só o que acontece com os dados reais da torre: eles formam duas linhas!
Coisas que você aprende na sua primeira aula de engenharia: se você faz o projeto de um elevador, e determina que o cabo do elevador precisa aguentar no mínimo 10 toneladas, qual o cabo que você coloca no elevador? Um matemático diria que é um cabo de 10 toneladas, mas o engenheiro vai falar que o mínimo são 14 toneladas.
Isso é o resultado do fator de segurança. Por mais que o seu modelo matemático seja correto, sempre tem alguma coisa que você não levou em conta (pode ser que o aço que você usou tenha impurezas, ou que o solo não é tão firme quanto você achava, e assim por diante). Por isso, é costume sempre multiplicar o valor final por um fator de segurança para levar em contas esses imprevistos.
O Eiffel sabia disso, e no diário ele explica que imaginava que a base da torre estaria sujeita a torques maiores que o topo, e por isso usou um fator de segurança diferente na base e no topo. Quando você faz o best fit com duas exponenciais ao invés de uma só, o gráfico fica bem melhor!
Agora finalmente podemos dar o mistério por resolvido: o formato da Torre Eiffel é descrito por duas exponenciais, escolhidas para minimizar o material necessário para resistir à carga do vento.
A Torre Eiffel é o literalmente o maior monumento à ciência construído, da próxima vez que passar por Paris aproveite para fazer uma reverência aos cientistas do passado :)

A torre mais alta do mundo
O desafio proposto pelo Gustave Eiffel era grandioso: construir a torre mais alta do mundo. Na época, o recorde era o Monumento de Washington, com 169 metros. O Eiffel pretendia erguer sua torre com 324 metros, quase o dobro do recorde anterior.
Para entender o desafio, vale a pena comparar a Torre Eiffel com outras torres da antiguidade. O desenho abaixo está em escala, e mostra a Torre Eiffel comparada com a Grande Pirâmide de Giza no Egito, e com o Campanário de São Marcos em Veneza:
Imagem: Wikipedia (CC-SA)
O primeiro desafio ao fazer uma torre é garantir que ela consiga suportar seu próprio peso. Os egípcios resolveram isso com força bruta: usaram blocos de pedra maciços e fizeram a base bem maior que o topo. O resultado final certamente funcionou, a pirâmide está aí de pé 4500 anos depois. Mas ela é um desperdício de material, com tecnologia moderna você não precisa de tanta matéria-prima para chegar nessa altura.
O Campanário de São Marcos é o extremo oposto. Ele foi construído em 1514, e nessa época a tecnologia já permitia criar uma torre com a largura da base igual à do topo. O problema é que a torre caiu! Em 1902 ela não resistiu ao próprio peso e colapsou (nenhuma vida humana foi perdida, mas o gato do zelador morreu). A torre que você visita hoje em Veneza é uma reconstrução.
Como fazer, então, uma torre alta que suporte o próprio peso? O Eiffel sabia a resposta porque tinha experiência no assunto. Antes de criar os ícones pelo qual é mais lembrado, ele construía pontes. Existem pontes do Eiffel por todo o mundo, desde a França e a Romênia, até o Vietnã e o Chile.
Para entender a tecnologia do Eiffel, vale a pena comparar com uma ponte antiga: a Pont du Gard, um aqueduto romano construído dois mil anos atrás. Ele cobre uma distância de 275 metros a uma altura de 48 metros. Para isso, ela precisa de cinco apoios no chão e três níveis de arcos para aguentar seu próprio peso:
Imagem: Wikipedia (CC-SA)
Agora, compare com uma das mais belas pontes construídas pelo Eiffel: a Ponte Dona Maria, na Cidade do Porto, em Portugal. Ela cobre 353m a 60m de altura, em ambos os casos maior que a ponte romana. E faz isso usando só dois apoios no chão! O segredo do Eiffel para conseguir esse feito é a magia da treliça. Ao usar uma treliça, você consegue suportar mais peso com menos material.
Todo mundo sabia que o Eiffel era expert no assunto, e que ele saberia construir uma torre que suportasse o próprio peso. Mas, ainda assim, na época ele ouviu muitas críticas. Uma coisa é você construir uma ponte na horizontal, outra é construir uma torre na vertical. Estruturas na vertical tem um problema adicional: será que o Eiffel sabia como fazer a torre resistir ao vento?
O método geométrico do Eiffel
Quando a torre ficou pronta, o Eiffel calou os críticos. Quem já visitou a torre sabe que no terceiro piso venta. Venta muito mesmo! Porém, a torre não se abala. Fica lá, imóvel, mesmo com os ventos mais fortes.
E qual foi o truque do Eiffel para deixar a torre tão estável com o vento? Até pouco tempo atrás, ninguém sabia. As plantas da torre Eiffel são conhecidas, você pode ver todas as especificações em um livrão publicado pela Taschen (todas mesmo, tem até o diâmetro e comprimento de cada parafuso). Mas as plantas não falam o truque da estabilidade, tudo que dizem é que o Eiffel determinou o formato da torre de forma a minimizar a ação do vento, e fez isso usando "métodos geométricos baseados em observações empíricas".
O formato da torre foi um mistério por mais de um século, até que Patrick Weidman, professor da Universidade de Colorado, matou o problema, e da maneira mais simples possível. Ele foi atrás dos diários do Eiffel e achou lá a dica que resolve o problema! O trecho do diário dizia:
"Suponha que as faces de uma treliça simples formam uma parede resistente às forças cisalhantes do vento, cujas componentes horizontais são P', P'', P''', P''''. Sabemos que, para calcular as forças atuantes no corte pelo plano MN, precisamos determinar a resultante P de todas as forças exteriores atuando acima da secção, e decompor essa resultante nas três forças passando pelas peças cortadas. Se a forma do sistema for tal que, para cada corte horizontal MN, a extensão das peças externas da treliça se intersectam na força exterior P, então as forças na barra interna serão zero e podemos excluir esse membro."
O diário tinha esse desenho acompanhando:
Lendo com cuidado dá para entender direitinho a motivação do formato da torre. Vamos recriar o raciocínio em câmera lenta. Nós começamos supondo que o vento é uma carga horizontal atuando sobre toda a torre (que ele representou como as forças P', P'', etc). O truque agora é pegar um corte horizontal arbitrário (que ele chamou de MN), e tirar toda a parte de cima da torre. As forças na estrutura não mudam se substituirmos a parte de cima por um ponto material de mesma massa, localizado no centróide do que foi tirado.
Vamos então ver qual é o efeito do vento. Eu tenho uma força P horizontal, que é a resultante do vento. Tenho ainda três forças F1, F2, F3, que são as forças atuando sobre as vigas da treliça. Quando uma treliça está em equilíbrio, as forças sobre ela são sempre de tração ou compressão, ou seja, estão na mesma direção de suas vigas respectivas.
A torre está em equilíbrio estático, logo a soma das forças é zero. Além disso, ela também não está rotacionando; logo a soma dos torques também é zero. O torque é o produto da força pela distância; mas não é qualquer distância, é a distância na direção perpendicular à força.
Agora o truque do Eiffel é claro. Ele construiu as laterais da torre de modo que as tangentes às vigas mais externas sempre passam pelo centróide. Quando você faz isso, a direção das forças P, F1 e F3 apontam para o centróide, então o torque delas é zero. Só a força F2 está aplicando torque no centróide!
Podemos calcular a soma dos torques agora. A distância associada à força F2 é a distância d, em verde na figura. Note que ela é estritamente positiva.
$$\begin{align*} P\times 0 +F_1\times 0+F_2\times d+F_3\times 0&=0\\ F_2\times d&=0\\ F_2&=0 \end{align*}$$
Ahá! Se as tangentes externas apontam para o centróide, então a força na viga interna é zero! Se o vento horizontal fosse a única força atuando sobre a torre, então nós poderíamos até tirar a viga interna que não faria diferença!
É claro que na prática não podemos tirar a viga. Ela não ajuda a resistir ao vento, mas ajuda a sustentar o peso. Por outro lado, essa viga pode ser mais fraca que as outras. Com a idéia do Eiffel, só as vigas externas precisam ser fortes. Nessa foto que eu tirei do pilar oeste isso é bem visível: as vigas externas são largas e feitas de material rígido, enquanto que as internas são finas e feitas de mini-treliças, o que deixa a estrutura como um todo mais leve. E quanto mais leve, mais alto você pode subir.
A equação da Torre Eiffel
Agora que nós sabemos o truque do Eiffel, podemos calcular qual é o lugar geométrico dos pontos cujas tangentes passam pelo centróide, isso vai nos dar a equação que descreve o fomato da torre. Aparentemente o Eiffel nunca precisou fazer isso, já que ele usou "um método geométrico baseado em observações empíricas" (para mim isso é um jeito de dizer que ele calculou uma solução numérica ao invés de resolver a equação de fato).
Mas ele poderia ter resolvido a equação se quisesse. Vamos fazer as contas na caixa azul para conferir, pule se você tem medo de equações diferenciais:
Começaremos supondo que o formato da torre pode ser descrito por uma função f(x). Para simplificar as contas (e, acredite, simplifica mesmo), nós vamos rotacionar o gráfico de modo a colocar o eixo x na vertical, orientado para baixo, e o f(x) na horizontal. Vamos ainda supor que f(x) é real, contínua e pode ser diferenciada muitas vezes.
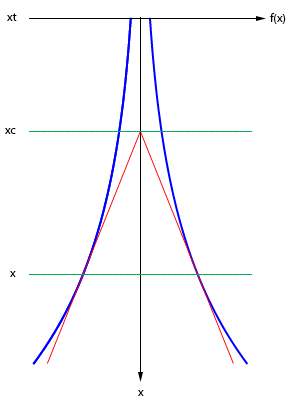
No gráfico acima, f(x) está desenhada em azul. Por um ponto qualquer x eu traço as retas tangentes (em vermelho), elas vão se encontrar em um ponto xC, que nós estamos supondo que sempre será o centróide da parte superior da torre (ou seja, do trecho que vai do ponto escolhido x, até o topo da torre xT). A posição do centróide é dado diretamente pela definição: $$x_C=\frac{\int_{x_T}^{x}t f(t)\,dt}{\int_{x_T}^{x} f(t)\,dt}$$ A tangente podemos calcular de duas maneiras. Nós sabemos que a tangente que passa por x é dada diretamente por f'(x). Por outro lado, ela também é a tangente do ângulo formado pelo eixo x e pela reta vermelha, que você calcula direto como cateto oposto pelo adjacente: $$f'(x)=\frac{\Delta y}{\Delta x}=\frac{f(x) -0}{x-x_C}=\frac{f(x)}{x-x_C}$$ Podemos isolar xC nessa última equação: $$\begin{align*} x-x_C&=\frac{f(x)}{f'(x)}\\ x_C&=\frac{x f'(x)-f(x)}{f'(x)} \end{align*}$$ E depois igualar as duas equações: $$\begin{align*} \frac{x f'(x)-f(x)}{f'(x)} &= \frac{\int_{x_T}^{x}t f(t)\, dt}{\int_{x_T}^{x} f(t)\, dt}\\ \left(x f'(x)-f(x)\right)\int_{x_T}^{x} f(t)\, dt &= f'(x)\int_{x_T}^{x}t f(t)\, dt\\ \left(f'(x)\int_{x_T}^{x}x f(t)\, dt \right)-\left(f(x)\int_{x_T}^{x} f(t)\, dt\right) &= f'(x)\int_{x_T}^{x}t f(t)\, dt\\ f(x)\int_{x_T}^{x} f(t)\, dt &= f'(x)\int_{x_T}^{x}(x-t) f(t)\, dt \end{align*}$$ Na última linha, veja que o x passou para dentro da integral, você pode fazer isso porque ele é constante em relação à variável de integração, que é t. Antes de prosseguir, vamos dar nomes às integrais, chamando-as de g(x) e h(x). Note que essas integrais são funções de x. $$\begin{align*} g(x)&=\int_{x_T}^{x} f(t)\, dt \\ h(x)&= \int_{x_T}^{x}(x-t) f(t)\, dt \end{align*}$$ Vamos substituir as integrais pelas funções que nomeamos, e depois derivar dos dois lados. Quando você deriva dos dois lados, você está comendo uma constante, então no final podem aparecer soluções espúrias. Depois de acabar tudo, temos que pegar as soluções e voltar para o começo, conferindo se elas são realmente válidas. $$\begin{align*} f(x)g(x)&=f'(x)h(x)\\ f'(x)g(x)+f(x)g'(x) &= f''(x)h(x)+f'(x)h'(x) \end{align*}$$ Como calcular g'(x) e h'(x)? Vamos começar por g'(x). Note, primeiro, que você pode usar o teorema fundamental do cálculo para escrever g(x) em função da primitiva de f(x), que iremos chamar de F(x): $$g(x)=\int_{x_T}^x f(t)\,dt=F(x) -F(x_T) $$ Já que F(xT) é uma constante, sua derivada é zero. F(x) é uma primitiva, e a derivada da primitiva de uma função é a própria função (desde que ela seja contínua): $$\begin{align*} g(x)&=F(x) -F(x_T)\\ g'(x)&=F'(x)-0=f(x) \end{align*} $$ Então g'(x)=f(x), essa foi fácil. Para calcular h'(x) é mais complicado. Lembremos a regra de integração por partes para integrais definidas: $$\begin{align*} \int_c^d a(t)b'(t)\,dt&=[a(t)b(t)]_c^d-\int_c^d a'(t)b(t)\,dt \end{align*} $$ Vamos escolher quem são a(t) e b(t): $$\begin{align*} a(t)=x-t&\implies a'(t)=-1\\ b(t)=F(t)&\implies b'(t)=f(t)\\ \end{align*} $$ Agora podemos quebrar h(x) em duas partes: $$\begin{align*} h(x)&=\int_{x_T}^x(x-t)f(t)\,dt\\ &=[(x-t)F(t)]_{x_T}^x-\int_{x_T}^x-F(t)\,dt\\ &=(x-x)F(x)-(x-x_T)F(x_T)+\int_{x_T}^xF(t)\,dt\\ &=-(x-x_T)F(x_T)+\int_{x_T}^xF(t)\,dt\\ &=-(x-x_T)F(x_T)+P(x)-P(x_T)\\ \end{align*} $$ No último passo, por falta de notação melhor, eu chamei de P(x) a primitiva de F(x). Agora podemos derivar h(x). Note que, se P(x) é a primitiva de F(x), então F(x) é a derivada de P(x). Além disso, como P(xT) é constante, sua derivada é zero: $$\begin{align*} h(x)&=-(x-x_T)F(x_T)+P(x)-P(x_T)\\ h'(x)&=-F(x_T)+F(x)-0\\ h'(x)&=\int_{x_T}^xf(t)\,dt\\ h'(x)&=g(x)\\ \end{align*} $$ Concluímos então que h'(x) é o mesmo g(x) que tínhamos visto antes! Antes de continuar, vale a pena resumir o que nós temos até agora: $$\begin{align*} f(x)g(x)&=f'(x)h(x)\\ f'(x)g(x)+f(x)g'(x) &= f''(x)h(x)+f'(x)h'(x)\\ f(x)&=g'(x)\\ f'(x)&=g''(x)\\ f''(x)&=g'''(x)\\ h'(x)&=g(x) \end{align*}$$ Note que dá para reescrever quase tudo usando só g(x) e suas derivadas. Fica faltando h(x), mas isso não é problema porque temos duas equações usando h(x), então é só isolar. Da primeira equação temos: $$\begin{align*} f(x)g(x)&=f'(x)h(x)\\ h(x)&=\frac{f(x)g(x)}{f'(x)}\\ h(x)&=\frac{g'(x)g(x)}{g''(x)}\\ \end{align*}$$ Da segunda equação, temos: $$\begin{align*} f'(x)g(x)+f(x)g'(x)&=f''(x)h(x)+f'(x)h'(x)\\ f''(x)h(x)&=f'(x)g(x)+f(x)g'(x)-f'(x)h'(x)\\ h(x)&=\frac{f'(x)g(x)+f(x)g'(x)-f'(x)h'(x)}{f''(x)}\\ h(x)&=\frac{g''(x)g(x)+g'(x)g'(x)-g''(x)g(x)}{g'''(x)}\\ h(x)&=\frac{g'(x)^2}{g'''(x)}\\ \end{align*}$$ Igualando as duas expressões para h(x): $$\begin{align*} \frac{g'(x)g(x)}{g''(x)} &= \frac{g'(x)^2}{g'''(x)} \\ \frac{g'(x)}{g(x)} &= \frac{g'''(x)}{g''(x)} \end{align*}$$ Tudo que falta agora é resolver a equação para g(x) e finalmente temos o formato da torre. Mas essa equação é uma equação diferencial não-linear de terceira ordem. E isso é os que os matemáticos usam para assustar os filhos: "se você não comer, vai aparecer o bicho-papão, o homem do saco e a equação diferencial não-linear de terceira ordem para te pegar!" Felizmente, essa equação pode ser resolvida se você tiver a visão além do alcance. O que acontece quando você tenta diferenciar log g(x)? $$\begin{align*} \frac{d}{dx}\log(g(x))=\frac{1}{g(x)}\times g'(x)=\frac{g'(x)}{g(x)} \end{align*}$$ Ahá! Essa é exatamente a forma da equação. Fazendo o análogo no outro lado, podemos reescrever a equação original: $$\begin{align*} \frac{g'(x)}{g(x)} &= \frac{g'''(x)}{g''(x)}\\ \frac{d}{dx}\log g(x) &= \frac{d}{dx}\log g''(x) \end{align*}$$ Agora nós podemos integrar dos dois lados (lembrando que vai aparecer uma constante), e depois tirar a exponencial dos dois lados: $$\begin{align*} \frac{d}{dx}\log g(x) &= \frac{d}{dx}\log g''(x)\\ \log g(x) &= \log g''(x) + C\\ g(x) &= k g''(x) \\ \end{align*}$$ Agora ficou fácil né? A equação medonha virou uma equação diferencial linear de segunda ordem, essa é bem-comportada, dá a patinha e finge de morta. A solução geral é da forma abaixo: $$g(x)=A e^{B x}+C e^{-B x}$$ Como f(x)=g'(x), então f(x) também tem a forma acima, só os coeficientes que serão diferentes. A natureza da função depende dos coeficientes; por exemplo, se A=0.5, C=0.5 e B=i, então f(x)=cos(x). Mas nem todas as combinações de coeficientes são soluções válidas! Para determinar os coeficientes corretos, precisamos voltar o f(x) lá na equação original: $$f(x)\int_{x_T}^{x} f(t)\, dt = f'(x)\int_{x_T}^{x}(x-t) f(t)\, dt $$ Daqui em diante é só fazer as contas. Se você substituir tudo, vai notar que o único jeito de conseguir uma solução real válida para qualquer x é fazendo C=0 e xT=-∞; nesse caso A pode ser um real qualquer, e B pode ser um real positivo qualquer. Estritamente falando, a torre teria que ser infinitamente alta para satisfazer a essa equação, mas na prática você pode aproximar "infinitamente alta" por "muito, muito alta". Concluindo, a solução final para o formato da torre Eiffel é: $$f(x)=A e^{B x} $$ Ou seja, a torre tem um perfil exponencial!

No gráfico acima, f(x) está desenhada em azul. Por um ponto qualquer x eu traço as retas tangentes (em vermelho), elas vão se encontrar em um ponto xC, que nós estamos supondo que sempre será o centróide da parte superior da torre (ou seja, do trecho que vai do ponto escolhido x, até o topo da torre xT). A posição do centróide é dado diretamente pela definição: $$x_C=\frac{\int_{x_T}^{x}t f(t)\,dt}{\int_{x_T}^{x} f(t)\,dt}$$ A tangente podemos calcular de duas maneiras. Nós sabemos que a tangente que passa por x é dada diretamente por f'(x). Por outro lado, ela também é a tangente do ângulo formado pelo eixo x e pela reta vermelha, que você calcula direto como cateto oposto pelo adjacente: $$f'(x)=\frac{\Delta y}{\Delta x}=\frac{f(x) -0}{x-x_C}=\frac{f(x)}{x-x_C}$$ Podemos isolar xC nessa última equação: $$\begin{align*} x-x_C&=\frac{f(x)}{f'(x)}\\ x_C&=\frac{x f'(x)-f(x)}{f'(x)} \end{align*}$$ E depois igualar as duas equações: $$\begin{align*} \frac{x f'(x)-f(x)}{f'(x)} &= \frac{\int_{x_T}^{x}t f(t)\, dt}{\int_{x_T}^{x} f(t)\, dt}\\ \left(x f'(x)-f(x)\right)\int_{x_T}^{x} f(t)\, dt &= f'(x)\int_{x_T}^{x}t f(t)\, dt\\ \left(f'(x)\int_{x_T}^{x}x f(t)\, dt \right)-\left(f(x)\int_{x_T}^{x} f(t)\, dt\right) &= f'(x)\int_{x_T}^{x}t f(t)\, dt\\ f(x)\int_{x_T}^{x} f(t)\, dt &= f'(x)\int_{x_T}^{x}(x-t) f(t)\, dt \end{align*}$$ Na última linha, veja que o x passou para dentro da integral, você pode fazer isso porque ele é constante em relação à variável de integração, que é t. Antes de prosseguir, vamos dar nomes às integrais, chamando-as de g(x) e h(x). Note que essas integrais são funções de x. $$\begin{align*} g(x)&=\int_{x_T}^{x} f(t)\, dt \\ h(x)&= \int_{x_T}^{x}(x-t) f(t)\, dt \end{align*}$$ Vamos substituir as integrais pelas funções que nomeamos, e depois derivar dos dois lados. Quando você deriva dos dois lados, você está comendo uma constante, então no final podem aparecer soluções espúrias. Depois de acabar tudo, temos que pegar as soluções e voltar para o começo, conferindo se elas são realmente válidas. $$\begin{align*} f(x)g(x)&=f'(x)h(x)\\ f'(x)g(x)+f(x)g'(x) &= f''(x)h(x)+f'(x)h'(x) \end{align*}$$ Como calcular g'(x) e h'(x)? Vamos começar por g'(x). Note, primeiro, que você pode usar o teorema fundamental do cálculo para escrever g(x) em função da primitiva de f(x), que iremos chamar de F(x): $$g(x)=\int_{x_T}^x f(t)\,dt=F(x) -F(x_T) $$ Já que F(xT) é uma constante, sua derivada é zero. F(x) é uma primitiva, e a derivada da primitiva de uma função é a própria função (desde que ela seja contínua): $$\begin{align*} g(x)&=F(x) -F(x_T)\\ g'(x)&=F'(x)-0=f(x) \end{align*} $$ Então g'(x)=f(x), essa foi fácil. Para calcular h'(x) é mais complicado. Lembremos a regra de integração por partes para integrais definidas: $$\begin{align*} \int_c^d a(t)b'(t)\,dt&=[a(t)b(t)]_c^d-\int_c^d a'(t)b(t)\,dt \end{align*} $$ Vamos escolher quem são a(t) e b(t): $$\begin{align*} a(t)=x-t&\implies a'(t)=-1\\ b(t)=F(t)&\implies b'(t)=f(t)\\ \end{align*} $$ Agora podemos quebrar h(x) em duas partes: $$\begin{align*} h(x)&=\int_{x_T}^x(x-t)f(t)\,dt\\ &=[(x-t)F(t)]_{x_T}^x-\int_{x_T}^x-F(t)\,dt\\ &=(x-x)F(x)-(x-x_T)F(x_T)+\int_{x_T}^xF(t)\,dt\\ &=-(x-x_T)F(x_T)+\int_{x_T}^xF(t)\,dt\\ &=-(x-x_T)F(x_T)+P(x)-P(x_T)\\ \end{align*} $$ No último passo, por falta de notação melhor, eu chamei de P(x) a primitiva de F(x). Agora podemos derivar h(x). Note que, se P(x) é a primitiva de F(x), então F(x) é a derivada de P(x). Além disso, como P(xT) é constante, sua derivada é zero: $$\begin{align*} h(x)&=-(x-x_T)F(x_T)+P(x)-P(x_T)\\ h'(x)&=-F(x_T)+F(x)-0\\ h'(x)&=\int_{x_T}^xf(t)\,dt\\ h'(x)&=g(x)\\ \end{align*} $$ Concluímos então que h'(x) é o mesmo g(x) que tínhamos visto antes! Antes de continuar, vale a pena resumir o que nós temos até agora: $$\begin{align*} f(x)g(x)&=f'(x)h(x)\\ f'(x)g(x)+f(x)g'(x) &= f''(x)h(x)+f'(x)h'(x)\\ f(x)&=g'(x)\\ f'(x)&=g''(x)\\ f''(x)&=g'''(x)\\ h'(x)&=g(x) \end{align*}$$ Note que dá para reescrever quase tudo usando só g(x) e suas derivadas. Fica faltando h(x), mas isso não é problema porque temos duas equações usando h(x), então é só isolar. Da primeira equação temos: $$\begin{align*} f(x)g(x)&=f'(x)h(x)\\ h(x)&=\frac{f(x)g(x)}{f'(x)}\\ h(x)&=\frac{g'(x)g(x)}{g''(x)}\\ \end{align*}$$ Da segunda equação, temos: $$\begin{align*} f'(x)g(x)+f(x)g'(x)&=f''(x)h(x)+f'(x)h'(x)\\ f''(x)h(x)&=f'(x)g(x)+f(x)g'(x)-f'(x)h'(x)\\ h(x)&=\frac{f'(x)g(x)+f(x)g'(x)-f'(x)h'(x)}{f''(x)}\\ h(x)&=\frac{g''(x)g(x)+g'(x)g'(x)-g''(x)g(x)}{g'''(x)}\\ h(x)&=\frac{g'(x)^2}{g'''(x)}\\ \end{align*}$$ Igualando as duas expressões para h(x): $$\begin{align*} \frac{g'(x)g(x)}{g''(x)} &= \frac{g'(x)^2}{g'''(x)} \\ \frac{g'(x)}{g(x)} &= \frac{g'''(x)}{g''(x)} \end{align*}$$ Tudo que falta agora é resolver a equação para g(x) e finalmente temos o formato da torre. Mas essa equação é uma equação diferencial não-linear de terceira ordem. E isso é os que os matemáticos usam para assustar os filhos: "se você não comer, vai aparecer o bicho-papão, o homem do saco e a equação diferencial não-linear de terceira ordem para te pegar!" Felizmente, essa equação pode ser resolvida se você tiver a visão além do alcance. O que acontece quando você tenta diferenciar log g(x)? $$\begin{align*} \frac{d}{dx}\log(g(x))=\frac{1}{g(x)}\times g'(x)=\frac{g'(x)}{g(x)} \end{align*}$$ Ahá! Essa é exatamente a forma da equação. Fazendo o análogo no outro lado, podemos reescrever a equação original: $$\begin{align*} \frac{g'(x)}{g(x)} &= \frac{g'''(x)}{g''(x)}\\ \frac{d}{dx}\log g(x) &= \frac{d}{dx}\log g''(x) \end{align*}$$ Agora nós podemos integrar dos dois lados (lembrando que vai aparecer uma constante), e depois tirar a exponencial dos dois lados: $$\begin{align*} \frac{d}{dx}\log g(x) &= \frac{d}{dx}\log g''(x)\\ \log g(x) &= \log g''(x) + C\\ g(x) &= k g''(x) \\ \end{align*}$$ Agora ficou fácil né? A equação medonha virou uma equação diferencial linear de segunda ordem, essa é bem-comportada, dá a patinha e finge de morta. A solução geral é da forma abaixo: $$g(x)=A e^{B x}+C e^{-B x}$$ Como f(x)=g'(x), então f(x) também tem a forma acima, só os coeficientes que serão diferentes. A natureza da função depende dos coeficientes; por exemplo, se A=0.5, C=0.5 e B=i, então f(x)=cos(x). Mas nem todas as combinações de coeficientes são soluções válidas! Para determinar os coeficientes corretos, precisamos voltar o f(x) lá na equação original: $$f(x)\int_{x_T}^{x} f(t)\, dt = f'(x)\int_{x_T}^{x}(x-t) f(t)\, dt $$ Daqui em diante é só fazer as contas. Se você substituir tudo, vai notar que o único jeito de conseguir uma solução real válida para qualquer x é fazendo C=0 e xT=-∞; nesse caso A pode ser um real qualquer, e B pode ser um real positivo qualquer. Estritamente falando, a torre teria que ser infinitamente alta para satisfazer a essa equação, mas na prática você pode aproximar "infinitamente alta" por "muito, muito alta". Concluindo, a solução final para o formato da torre Eiffel é: $$f(x)=A e^{B x} $$ Ou seja, a torre tem um perfil exponencial!
Matemática e Engenharia
Agora que sabemos qual o formato teórico da torre, podemos usar os dados reais da torre para estimar os coeficientes da exponencial. Eu rodei um best fit e cheguei em A=3.34323 e B=0.0102592:

A aproximação é boa, mas... parece que não encaixa direitinho? É meio frustrante fazer esse monte de contas, e no fim a curva real não ser tão parecida assim com a equação deduzida.
Mas tem um motivo para isso, e o motivo é que o Eiffel era engenheiro, não matemático. Quando você plota uma exponencial em um gráfico semi-log, o resultado tem que ser uma linha. Mas olha só o que acontece com os dados reais da torre: eles formam duas linhas!
Coisas que você aprende na sua primeira aula de engenharia: se você faz o projeto de um elevador, e determina que o cabo do elevador precisa aguentar no mínimo 10 toneladas, qual o cabo que você coloca no elevador? Um matemático diria que é um cabo de 10 toneladas, mas o engenheiro vai falar que o mínimo são 14 toneladas.
Isso é o resultado do fator de segurança. Por mais que o seu modelo matemático seja correto, sempre tem alguma coisa que você não levou em conta (pode ser que o aço que você usou tenha impurezas, ou que o solo não é tão firme quanto você achava, e assim por diante). Por isso, é costume sempre multiplicar o valor final por um fator de segurança para levar em contas esses imprevistos.
O Eiffel sabia disso, e no diário ele explica que imaginava que a base da torre estaria sujeita a torques maiores que o topo, e por isso usou um fator de segurança diferente na base e no topo. Quando você faz o best fit com duas exponenciais ao invés de uma só, o gráfico fica bem melhor!
Agora finalmente podemos dar o mistério por resolvido: o formato da Torre Eiffel é descrito por duas exponenciais, escolhidas para minimizar o material necessário para resistir à carga do vento.
A Torre Eiffel é o literalmente o maior monumento à ciência construído, da próxima vez que passar por Paris aproveite para fazer uma reverência aos cientistas do passado :)