Dia desses a Giseli me pediu para escrever alguma coisa sobre o Riemann. Naturalmente eu topei, até porque eu e o Riemann temos uma anedota em comum! Georg Riemann nasceu em 1826, em uma linhagem de pastores luteranos: seu pai, avô e bisavô eram pastores. Desde cedo ele sempre ia muito bem na escola, a ponto do pai dele ter que contratar um professor particular, porque só a escola comum não era o suficiente para ele. Mas isso também não ajudou muito, em certo ponto o tutor disse que estava aprendendo com o Riemann mais do que estava ensinando para ele. A solução foi achar uma escola melhor.
Aos quatorze anos, o Riemann saiu de casa para ir morar com a avó, ficando assim muito mais perto do respeitável Gymnasium de Hannover, o melhor da região. E é aqui que as nossas histórias se interceptam, eu também saí de casa aos quatorze para ir morar com a avó, mas no meu caso foi para estudar na respeitável ETFSP (que hoje em dia chama IFSP).
Depois de conseguir seu doutorado, o Riemann tentou uma posição de professor na mesma universidade do Gauss. Como teste de admissão, o Gauss pediu para que ele escrevesse uma redação. Mas teria que ser sobre um tema que ambos gostassem, então a proposta foi a seguinte: o Riemann iria sugerir três tópicos, e dos três o Gauss escolheria qual seria o tema da redação. Os temas que o Riemann escolheu foram:
- Séries de Fourier
- Sistemas de Equações Quadráticas
- Fundamentos da Geometria
Os Elementos de Euclides
Pelo menos até metade do século 20, Elementos de Euclides era o segundo livro mais publicado no mundo, perdendo só para a Bíblia (mas hoje em dia ele deve ter perdido para o Harry Potter e o Crepúsculo).
Um dos motivos de ser um livro tão publicado é que trata-se de um livro muito didático, começando de princípios bem simples, e construindo em cima deles teoremas cada vez mais complexos. Tem um motivo para o livro ser assim: Euclides era professor, e os Elementos são a apostila com notas de aula! Provavelmente poucos teoremas do livro são de autoria dele, o mérito do Euclides foi reunir todos os trabalhos da época e colocar em notação consistente. Infelizmente, os originais de onde o Euclides tirou os teoremas foram todos destruídos nos muitos incêndios da Grande Biblioteca de Alexandria.
- Por dois pontos você sempre pode traçar uma reta.
- Um segmento de reta sempre pode ser estendido indefinidamente.
- Dado um centro e um raio, você sempre pode construir um círculo.
- Todos os ângulos retos são congruentes.
- Se você desenhar duas retas que intersectam uma terceira, de maneira que o ângulo interno em um dos lados seja menor que dois ângulos retos, então as duas linhas originais necessariamente se intersectam nesse lado, se você as estender o suficiente.
Lobachevsky e Bolyai
Como você tentaria provar a quinta proposição? A maneira mais natural é tentar um ataque por contradição: você assume o contrário do que quer provar, e tenta chegar numa contradição. Assumindo a negação da proposição, você conclui um monte de fatos que são intuitivamente absurdos. Por exemplo, que dado uma reta, existem infinitas retas paralelas a ela passando por um ponto dado, que o teorema de Pitágoras é falso, que a soma dos ângulos internos de um triângulo é menor que 180 graus.
Mas apesar de serem absurdos, nenhum desses fatos é uma contradição de verdade. Para a demonstração funcionar, você precisa de algum fato que contradiga os quatro princípios iniciais dos Elementos. Contradizer o que vem depois no livro não serve! Foi nesse ponto que, de maneira independente, o russo Lobachesvsky e o húngaro Bolyai tiveram um insight: e se na verdade a quinta proposição fosse independente das demais? Ou seja, tanto faz se você usa ela do jeito original ou a sua negação, o sistema continua consistente do mesmo jeito?
Isso é a base do que hoje chamamos de geometrias não-Euclideanas. Essa era uma idéia chocante para a época, de que podem existir geometrias que funcionam apesar de não seguirem todas as regras dos Elementos. O pai do Bolyai ficou tão orgulhoso com o resultado do filho que mandou uma carta pro Gauss avisando da descoberta. O Gauss respondeu "olha, eu não posso elogiar seu filho, porque eu tive a mesma idéia 30 anos atrás, e seria indelicado elogiar a mim mesmo."
A Curvatura de Gauss
Tecnicamente falando, era verdade. O Gauss realmente tinha pensado nisso, mas ele nunca publicou o resultado porque achou que era uma bobagem. Eu não tenho como saber o que se passava na cabeça dele, mas imagino que foi algo assim: "Essa geometria é perversa, se eu assumir que ela existe, então a soma dos ângulos internos do triângulo dá menos de 180 graus, e isso só seria verdade se o plano fosse curvo, o que é um absurdo. Por outro lado, eu posso usar isso para definir o que é curvatura de uma superfície! Eu defino então a curvatura intrínseca de uma superfície como sendo uma função de quanto a soma dos ângulos desvia de 180 graus."
Depois de definir o que é curvatura intrínseca, o Gauss provou uma proposição tão legal que ele chamou de Theorema Egregium (em português é Teorema Incrível, e se o Gauss chamou de incrível é porque a coisa é quente mesmo). O enunciado é assim:
"A curvatura intrínseca de uma superfície depende só das distâncias entre os pontos, e não de suas posições".
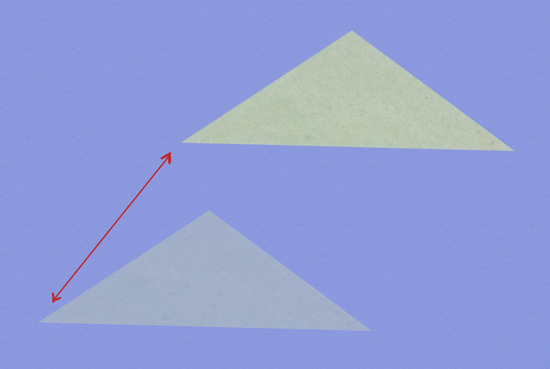
Isso parece... óbvio? Quer dizer, imagine que recorto um triângulo de papel reciclado como o abaixo:
Se eu mudar a posição dos pontos, por exemplo, fazendo uma translação, obviamente a soma dos ângulos do triângulo não muda:
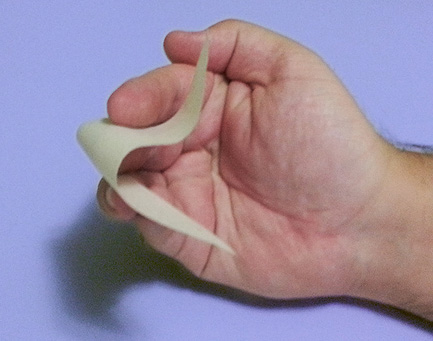
Mas a sacada do Gauss é que você pode torcer o triângulo sem mudar a soma de seus ângulos! Torcer o triângulo sem esticar é a mesma coisa que transladar cada ponto para um lugar diferente.
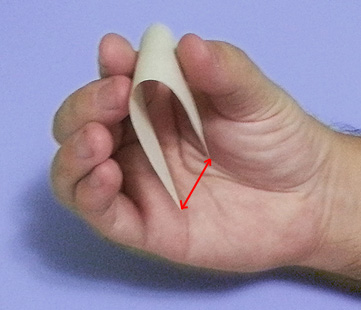
Mas peraí, se você torceu o triângulo, então você mudou as distâncias entre os pontos! Por exemplo, nessa imagem, fica claro que o caminho entre os vértices indicados é menor que do seria se o triângulo não estivesse torcido!
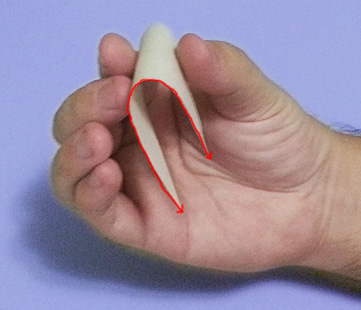
Mas para o Gauss, o que importa é a distância que uma formiga faria se estivesse andando no seu triângulo. Formiga não voa, ela precisa andar pelo papel, e por isso a distância que ela percorre é a mesma.
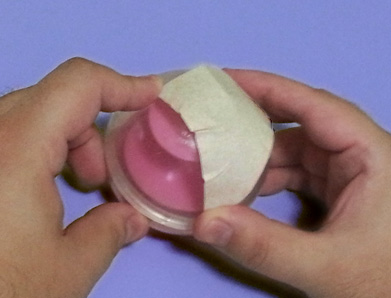
Com isso, você consegue mostrar que a curvatura do plano é diferente da curvatura da esfera. Eu tentei colocar o meu triângulo numa bolinha roubada da gata Luvinha, e olhe o que acontece: se eu tento forçar um dos lados do triângulo a ficar na esfera, o outro vértice vai para fora.
E se eu tento forçar todos os vértices a ficarem na bola, o papel amassa. Claramente, a distância de formiga entre dois pontos na esfera é sempre menor ou igual à distância de formiga sobre o plano, não importando como eu tento encaixar o plano.
Mas a parte menos intuitiva é que eu posso colocar o triângulo sobre uma latinha de Schweppes sem amassar o papel! A lateral do cilindro tem curvatura igual à do plano, então os ângulos dos triângulos sobre o cilindro somam sempre 180 graus.
Isso tem uma conseqüência prática interessante. Como a curvatura intrínseca do cilindro é igual à do plano, eu posso colocar um rótulo de Coca Zero na mesa sem amassar.
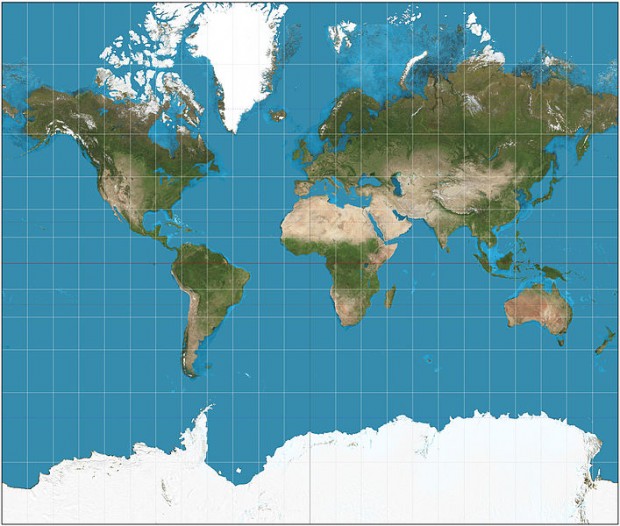
Mas não dá para fazer isso com a superfície de um globo! Por isso, todo mapa-mundi necessariamente introduz algum tipo de distorção, como a projeção de Mercator, que distorce horrivelmente a Antártica e a Groenlândia:
A Redação de Riemann
Agora já temos como entender o que o Riemann escreveu na sua redação. O título era "Über die Hypothesen welche der Geometrie zu Grunde liegen" (Sobre as hipóteses que formam a base da geometria), e tem uma tradução online para quem quiser ler. Note que não é um paper, é uma redação mesmo! Tem só uma fórmula e o resto é praticamente só texto.
A idéia principal do Riemann é a seguinte: segundo o Lobachevsky e o Bolyai, existem geometrias não-Euclideanas onde o espaço é curvo. Já segundo o Gauss, a curvatura do espaço depende da distância entre os pontos. Então podemos usar a função que mede distâncias para definir a geometria usada.
Por exemplo, na geometria clássica de Euclides, a distância entre dois pontos é dada pelo teorema de Pitágoras, cuja versão diferencial é a abaixo:
Mas eu posso extrapolar essa fórmula, por exemplo, adicionando outros tipos de dependências:
Cada um dos gij pode ser um número qualquer, ou até uma função qualquer! Quando escrito em forma tensorial, essa equação acima define o tensor métrico de Riemann. E a partir dele podemos derivar todas as outras características da geometria, incluindo a curvatura intrínseca em cada ponto.
Quando o Gauss leu a redação, quase esboçou um meio sorriso! (Diz a lenda que essa foi a única vez que Gauss elogiou um aluno em público. Era marrento esse Gauss). O Riemann foi admitido como professor, e trabalhou em diversas áreas, incluindo teoria dos números, onde enunciou a lendária hipótese de Riemann, um problema que está em aberto até hoje (e paga um milhão de dólares para quem resolver).
Mas, para mim, a parte mais profética da redação do Riemann são os parágrafos finais. Eu vou traduzir esse trecho final:
"Supondo que os corpos existem independentemente da posição, então a curvatura é constante em todo ponto, e segue pelas medidas astronômicas que não pode ser diferente de zero, ou ao menos que seu inverso seja uma área tal que o alcance de nossos telescópios seja desprezível. Mas se essa independência dos corpos da posição não existe, então não podemos tirar conclusões das relações métricas entre distâncias grandes e infinitamente pequenas; nesse caso a curvatura em cada ponto pode ter um valor arbitrário em três dimensões, desde que a curvatura total de cada porção mensurável do espaço não seja muito diferente de zero."
É isso. Em 1854, o Riemann cantou a bola da Relatividade Geral. Só faltou o Einstein deduzir, sessenta anos depois, que a tal curvatura variável em cada ponto era uma função da massa, e daí segue naturalmente que a gravidade é uma deformação do espaço-tempo. Nada mal para o menino que saiu aos 14 anos de casa para estudar!





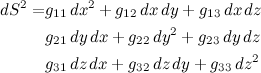
Nenhum comentário:
Postar um comentário